​

Education, Innovation, & Research (EIR)

The Education Innovation and Research (EIR) Program provides funding to:

• create, develop, implement, replicate, or take to scale entrepreneurial, evidence-based, field-initiated innovations to improve student achievement and attainment for high-need students; and
• rigorously evaluate such innovations.

The EIR program is designed to generate and validate solutions to persistent educational challenges and to support the expansion of effective solutions to serve substantially larger numbers of students.  The EIR is established under section 4611 of the Elementary and Secondary Education Act (ESEA), as amended by Every Student Succeeds Act (ESSA).

There are three types of grants under this program:

• “Early-phase” grants,
• “Mid-phase” grants, and
• “Expansion” grants.

These grants differ in terms of the level of prior evidence of effectiveness required for consideration for funding, the expectations regarding the kind of evidence and information funded projects should produce, the level of scale funded projects should reach, and, consequently, the amount of funding available to support each type of project.

Source: US Department of Education - Education, Innovation, & Research (EIR)

Early-phase EIR Grant:
Building Toward Computer Science Equity and Inclusion: Developing an Ecosystem of Supports 

While the nation is projected to become majority-minority by 2044, Orange County (OC), California (the 6th largest County in the US by population) reached that milestone in 2004. Skills in highly technical or creative occupations, such as those in STEM fields, need to be cultivated for the future workforce to stay relevant (Orange County Workforce Indicators Report, 2020). Home to Disney, Boeing, Parker Aerospace, and Edwards Lifesciences, OC has long been fertile soil for new, transformative ideas. OC’s diversity is a major asset to the global economy, but notable inequities and disparities exist. This presents opportunities to demonstrate breakthroughs in computational and design thinking for female students and students of color,who are historically underrepresented in STEM.

Our project has been following a cohort of students, beginning in their 9th grade year, and going through 11th grade.  Each year, our team engages a cohort of educators who is currently serving this group of students.  Educators have opportunities to expand their knowledge related to computational thinking practices, and are tasked with consciously incorporating these practices into two units over the course of the school year.  Additionally, our team focuses on building strategies to help students to be aware of the opportunities available to them, and to build a sense of STEM and computer science identity in all students, so that all students are keenly aware that they can study computer science, should they desire to do so.

Computational Thinking

"Computational thinking is a fundamental skill for everyone, not just for computer scientists. To reading, writing, and arithmetic, we should add computational thinking to every child’s analytical ability" (a).  In her groundbreaking essay Computational Thinking, Wing helped to popularize computational thinking as a multi-faceted cross-disciplinary approach to: analysis, solution-finding, and design.  Computational thinking serves as a cognitive and disciplinary foundation, on which learners may choose to build an understanding of computer science.  Our project focuses on the integration of computational thinking practices into core mathematics and science, and how these practices feed into computer science coursework.

"A primary motivation for introducing CT practices into science and mathematics classrooms is in response to the increasingly computational nature of the disciplines as they are practiced in the professional world (b). Computation is now an indispensable component of STEM disciplines (c). This rise in importance of CT and its constituent skills and practices has been recognized both by those creating standards for mathematics and science classrooms (d) as well as by computer science education organizations (e). Bringing computational tools and practices into mathematics and science classrooms gives learners a more realistic view of what STEM fields are and better prepares students for STEM careers (f).

Preparing students for the modern STEM landscape is not the only reason to bring CT into STEM classrooms. From a pedagogical perspective, the thoughtful use of computational tools and skillsets can deepen learning of STEM content (g). The reverse is also true – namely, that science and mathematics provides a meaningful context (and set of problems) within which CT can be applied (h). This differs markedly from teaching CT as part of a standalone course where the assignments tend to be divorced from real-world problems and applications. This reciprocal relationship—using computation to enrich STEM learning and using STEM to enrich computational learning—is at the heart of our motivation to bring CT and STEM together. A third motivation for bringing CT into STEM classrooms is to reach the widest possible audience and address the longstanding issues of underrepresentation of women and minorities in computational fields. Despite numerous ongoing local, regional, and national campaigns targeting women and underrepresented minorities, the numbers continue to drop in STEM (i) and computer science (j) enrollments. Among the reasons for these trends, researchers have identified a lack of interest and confidence (k), limited visibility of positive role models (l), and lack of positive experiences with both computer science and in STEM fields more broadly (m). Currently, only a fraction of high school students have the opportunity to take a computer science course due to a lack of qualified teachers, inadequate facilities, or a lack of student interest. Embedding CT activities in STEM coursework directly addresses the issue of students self-selecting into (or out of) computational learning experiences. It also avoids practical issues of fitting new classes into overcrowded schedules and finding teachers to teach them. Collectively, these aspects of the relationship between CT and STEM, paired with the ability to reach diverse audiences and work within existing educational infrastructure, makes the embedded CT design a potentially powerful and effective approach to bring CT to diverse learners."

(Orton et al., 2016)

References (from Orton et al.):
(a) Wing, 2006
(b) Education Policy Committee, 2014; Foster, 2006; Malyn-Smith & Lee, 2012; Weintrop et al., 2016
(c) Henderson, Cortina, & Wing, 2007
(d) National Governors Association Center for Best Practices, Council of Chief State School Officers, 2010; NGSS Lead States, 2013
(e) ACM/IEEE-CS Joint Task Force on Computing Curricula, 2013
(f) Augustine, 2005; Gardner, 1983
(g) Guzdial, 1994; National Research Council, 2011; Repenning, Webb, & Ioannidou, 2010; Sengupta et al., 2013; Wilensky, Brady, & Horn, 2014; Wilensky & Reisman, 2006
(h) Hambrusch et al., 2009; Jona et al., 2014; Lin et al., 2009; Wilensky et al., 2014
(i) National Science Board, 2012
(j) Klawe and Levenson, 1995
(k) Margolis, Fisher, & Miller, 2000
(l) Townsend, 2002
(m) AAUW, 1994; Miliszewska, Barker, Henderson, & Sztendur, 2006

Computational Thinking for Mathematics and Science Taxonomy

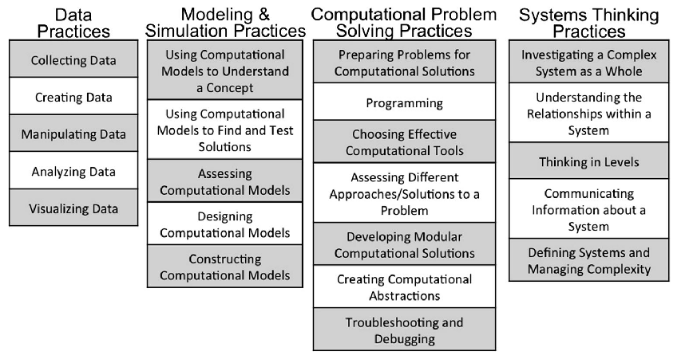
(Weintrop et al., 2016)

Computational Thinking for Mathematics and Science Taxonomy - Educator Handouts

Educator Experiences

References:

Orton, K. et al. (2016). Bringing computational thinking into high school mathematics and science classrooms. In C-K. Looi, J. L. Polman, P. Reimann, & U. Cress (Eds.), 12th International Conference of the Learning Sciences, ICLS 2016: Transforming Learning, Empowering Learners, Proceedings (Vol. 2, pp. 705-712). International Society of the Learning Sciences (ISLS).

Weintrop, D. et al. (2016). Defining computational thinking for mathematics and science classrooms. Journal of Science Education and Technology, 25(1), 127–147. https://doi.org/10.1007/s10956-015-9581-5

Wing, J. M. (2006). Computational thinking. Communications of the ACM, 49(3), 33–35. https://doi.org/10.1145/1118178.1118215

Legal Disclaimer & Licensing:

The contents of this website were developed under a grant from the US Department of Education.  However, these contents do not necessarily represent the policy of the US Department of Education, and one should not assume endoresement of policies by the US Federal Government.